Proof based on right-angle triangles
Any similar triangles have the property that if we select the same angle in all them, the ratio of the two sides defining the angle is the same regardless of which similar triangle is selected, regardless of its actual size: the ratios depend upon the three angles, not the lengths of the sides. Thus for either of the similar right triangles in the figure, the ratio of its horizontal side to its hypotenuse is the same, namely cos θ.The elementary definitions of the sine and cosine functions in terms of the sides of a right triangle are:
To complete the proof, the identities found at Trigonometric symmetry, shifts, and periodicity may be employed. By the periodicity identities we can say if the formula is true for −π < θ ≤ π then it is true for all real θ. Next we prove the range π/2 < θ ≤ π, to do this we let t = θ − π/2, t will now be in the range 0 < t ≤ π/2. We can then make use of squared versions of some basic shift identities (squaring conveniently removes the minus signs):
Related identities
The identitiesTabulation of derivations
Another way of thinking about the other identities is to derive them from the original identity. The following table shows how this is done by dividing each element of the original Pythagorean Identity by a common divisor.| Original Identity | Divisor | Divisor Equation | Derived Identity | Derived Identity (Alternate) |
|---|---|---|---|---|
 |
||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Proof using the unit circle
Main article: unit circle

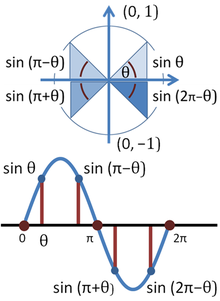
Point P(x,y) on the circle of unit radius at an obtuse angle θ > π/2
In the figure, the point P has a negative x-coordinate, and is appropriately given by x = cosθ, which is a negative number: cosθ = −cos(π−θ ). Point P has a positive y-coordinate, and sinθ = sin(π−θ ) > 0. As θ increases from zero to the full circle θ = 2π, the sine and cosine change signs in the various quadrants to keep x and y with the correct signs. The figure shows how the sign of the sine function varies as the angle changes quadrant.
Because the x- and y-axes are perpendicular, this Pythagorean identity is actually equivalent to the Pythagorean theorem for triangles with hypotenuse of length 1 (which is in turn equivalent to the full Pythagorean theorem by applying a similar-triangles argument). See unit circle for a short explanation.
Proof using power series
The trigonometric functions may also be defined using power series, namely (for x an angle measured in radians):[4][5]The Pythagorean theorem is not closely related to the Pythagorean identity when the trigonometric functions are defined in this way; instead, in combination with the theorem, the identity now shows that these power series parameterize the unit circle, which we used in the previous section. Note that this definition actually constructs the sin and cos functions in a rigorous fashion and proves that they are differentiable, so that in fact it subsumes the previous two.
Proof using the differential equation
Sine and Cosine can be defined as the two solutions to the differential equation:[6]A similar proof can be completed using power series as above to establish that the sine has as its derivative the cosine, and the cosine has as its derivative the negative sine. In fact, the definitions by ordinary differential equation and by power series lead to similar derivations of most identities.
This proof of the identity has no direct connection with Euclid's demonstration of the Pythagorean theorem.
sumber : http://en.wikipedia.org/wiki/Pythagorean_trigonometric_identity